Artificial Neural Networks (ANNs)
What are ANNs?
Traditional ML (machine learning) is dependent on learning or extracting features and patterns from a given set of data, tweaking a set of values (called weights and bias) which can help us make predictions when given new previously unseen data. When using this approach, we must manually identify the most optimal set of features which help ensure the most accurate predictions. However, Deep Learning uses artificial neural networks (ANNs) to automatically learn from large amounts of data. ANNs are like a computer version of the human brain, made up of many interconnected neurons that process information. A deep neural network has many layers of neurons that allow it to learn complex patterns in the data it’s given.
Each neuron in a neural network receives input from the previous layer of neurons and applies a simple mathematical function to that input, before passing its output on to the next layer. As data flows through the network, the weights of the connections between neurons are adjusted to minimize the difference between the predicted output and the actual output.
Under The Hood: Layer by Layer
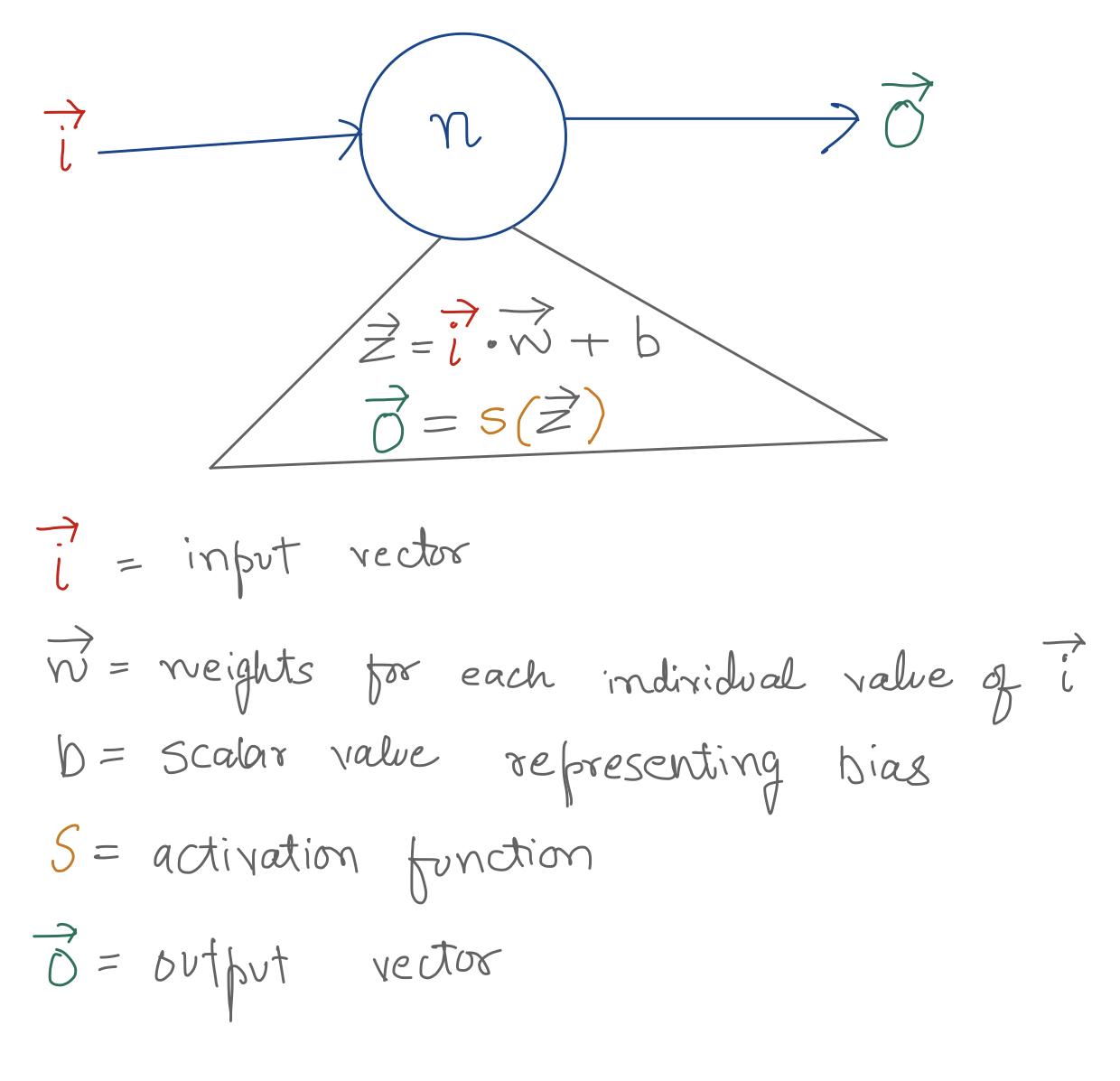
Perceptron is a single neuron that takes an input vector, applies a simple mathematical function to each value of that input, to produce an output vector. Usually, an activation function is also applied to each value of the output vector to handle non-linearity and enable the model to ascertain important neurons from the layer.
In a typical ANN, there are multiple layers of such neurons:
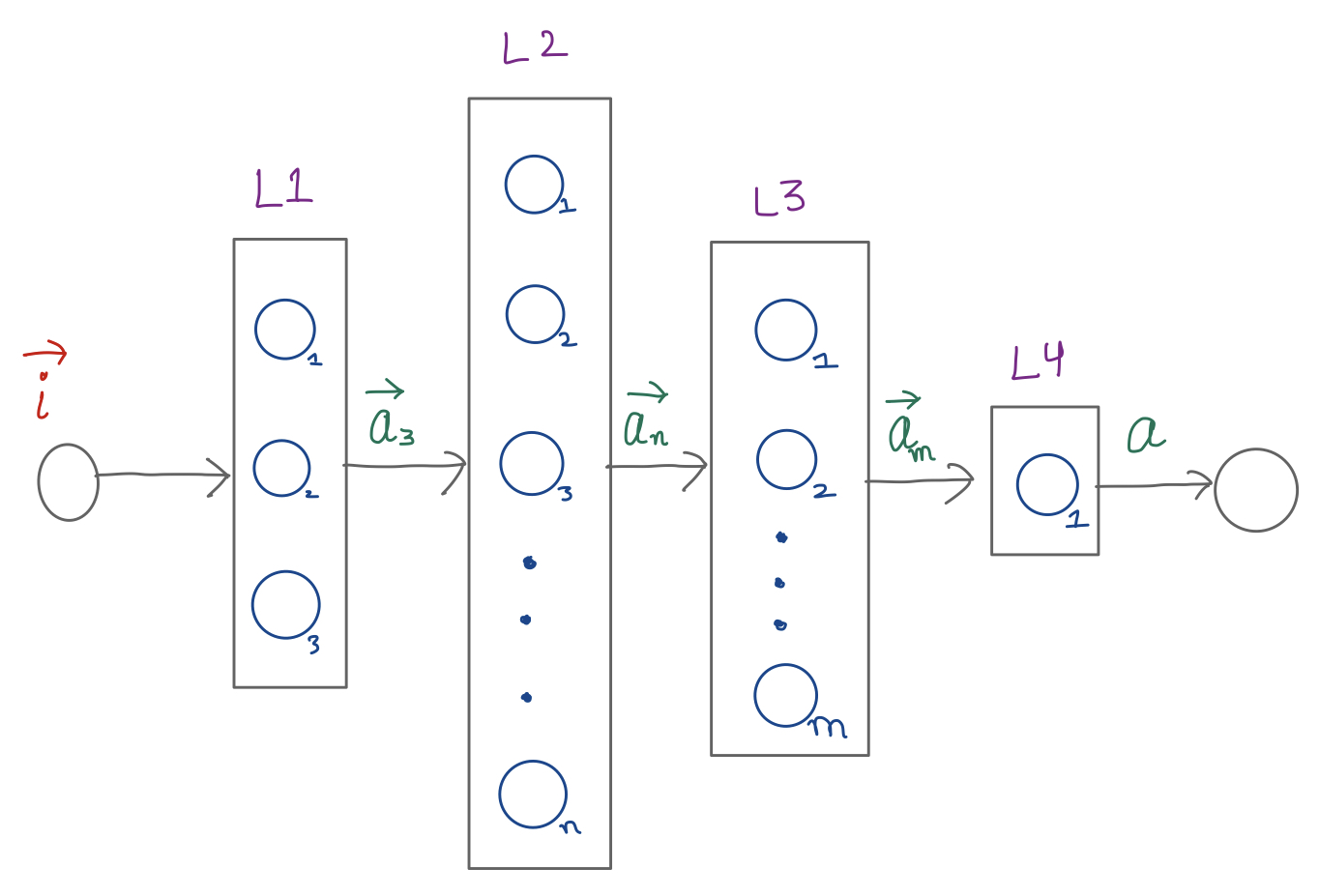
Each neuron in each layer takes as input a vector and produces a scalar value often called an activation value. All such activation values are composed in a vector which is then supplied to the neurons in the next layer.
Layer 0
Vector \(\vec{i}\) is the input vector which gets fed into the first layer (L1) of the NN. The values of these input vector is derived from the training dataset. These are the values being used to make predictions on, and are similar in nature to the values that the model will eventually be tested and used against.
\[\vec{i} = <x_1, x_2, x_3, ..., x_t>\]
Layer 1
Below image shows how L1 might look under the hood:

The output vector \(\vec{a_3}\) is then fed into Layer 2.
Layer 2
Layer 2, similar to layer 1, takes an input vector, which is fed to each neuron in its layer, producing a scalar value. This scalar value represents the activation value produced by each perceptron in that layer. All these values are than combined into the output vector \(\vec{a^2_n}\).

Layer 4
Layer 3 functions similar to Layer 1 and 2, however, notice that Layer 4 takes in as input a vector from previous layer, and outputs a scalar value in case of this NN example.
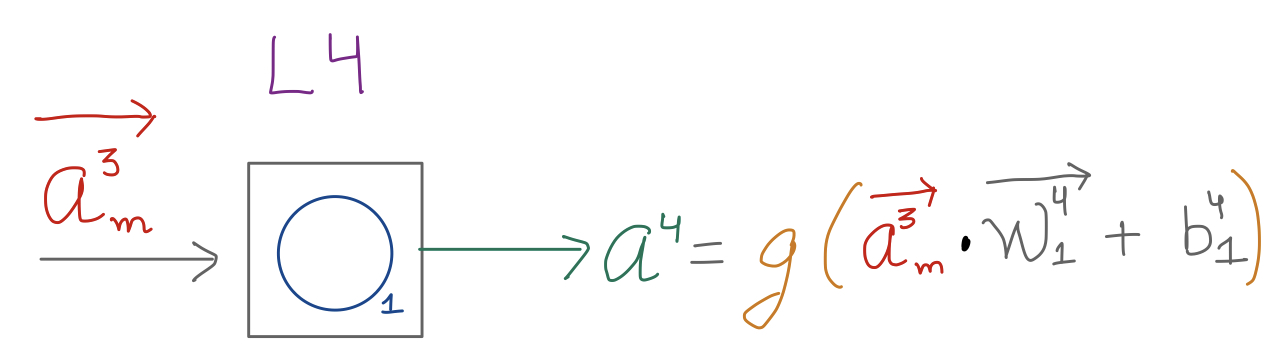
In the last layer, usually though not always, we use a sigmoid activation function, which gives us a value between 0 and 1, thereby helping us ascertain the probability of an event happening or not happening (i.e. the predicition)
Summary
ANNs deduce on their own the features that help the model be more accurate, so there is no need of manual feature engineering or scaling, which enables creation of efficient models with large number of (> millions) features.
To learn more about how activation functions works and different types of activation functions, check: Understanding Activation Functions in Depth